润格装饰

潘洛斯阶梯(Penrose Stairs)，曾出现在电影《盗梦空间》(Inception)里面的清醒梦境(lucid dream)中。

Arthur 展示给Ariadne看的奇怪阶梯，以及Arthur绕到佣兵背后的楼梯间，这是一座无限循环的阶梯。这种不可能出现的物体来自于将三维物体描绘于二维平面时出现的错视现象。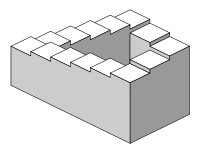潘洛斯阶梯 其名称Penrose来自于英国数学物理学家罗杰·潘洛斯(Roger Penrose)，他于1950年代设计了Penrose triangle，潘洛斯写了几篇文章讨论这些所谓的不可能事件，[1] On the Cohomology of Impossible Figure这篇短文讨论了这些对象的群的上同调。

Penrose stairs可视为Penrose triangle的一种变形。有名的Penrose stairs出现在荷兰艺术家M. C. Escher的版画Ascnding and Descending，以及Waterfall。

本来这些对象不可能实际在三维空间构造出来，因为这些错视和观看角度密切相关，不过可以利用计算机3D绘图做到很接近的程度，毕竟观看者看到的依旧是显示在二维平面屏幕上的图像。